ミームの死骸を待ちながら

We are built as gene machines and cultured as meme machines, but we have the power to turn against our creators. We, alone on earth, can rebel against the tyranny of the selfish replicators. - Richard Dawkins "Selfish Gene"

We are built as gene machines and cultured as meme machines, but we have the power to turn against our creators.
We, alone on earth, can rebel against the tyranny of the selfish replicators.
- Richard Dawkins "Selfish Gene"

ベイズの定理と条件付き確率についての覚書

math

前口上

条件付き確率を調べていてふいに「ベイズの定理ってもしかして大したこと言ってないのでは」と気がついたので, 将来記憶を失った自分に説明するイメージで記録する.

条件付き確率

まずベイズの定理は確率論における「条件付き確率(conditional probability)」に立脚しているので先に説明する.

条件付き確率とは, 事象Aが起こった条件下において事象Bが起こる確率のこと. たとえば

  • 雨が降る確率をP(雨)
  • 交通事故の発生確率をP(事故)

としたとき, 雨が降っている日に(= 雨が降っているという条件下において)交通事故が発生する確率を

P(事故|雨)

と表すことに決める. これが条件付き確率である.

記法について: P(B|A)は英語だと “the conditional probability of B given A” あるいは “the probability of B under the condition A” と読むらしい.

例をでっち上げてベン図を書いてみる.

  • 1年365日のなかで
  • 雨が降った日が100日
  • 事故が発生した日が67日
  • 雨が降っていて事故が発生した日が29日

と仮定すると(値の妥当性についてはとりあえず目を瞑って欲しい)以下のようになる*1.

f:id:Hash:20141203022836p:plain

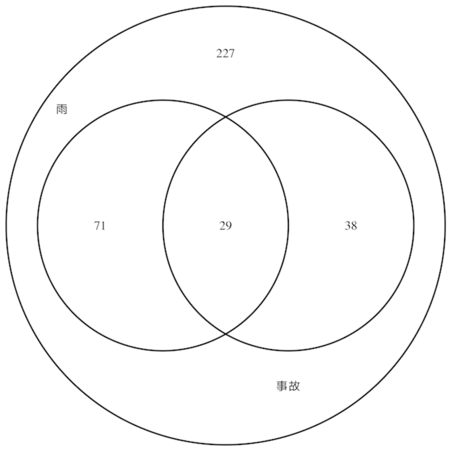
以上の数値を使えば条件付き確率の値が求められる…のだけど, その前に一瞬だけ同時確率の話をする.

同時確率

同時確率(joint probability)は中高数学から馴染みがある話だと思う. サイコロ2個振って同時に1の目が出るっちゅーアレ. 今回使っている例でいうと「事故が起き, かつ雨も振っている確率」が同時確率で,

P(事故,雨) もしくは P(事故 \cap雨)

と表す. カンマで並べてはいるけど順序に意味はなくP(A,B)はP(B,A)に等しい. 同時確率は母数(365日)のうち「雨が振っており事故が発生した」29日の占める割合であり,

P(事故,雨) = \frac{29}{365} \simeq 0.08

となる. 8%ですね. 条件付き確率との間には

  • 「事故が起こる確率. 分母は雨が振っている日」が条件付き確率.
  • 「事故が起こり雨も振っている確率. 分母は365日」が同時確率.

という違いがあるけど言葉で表すと混乱しがちかもしれない. 後で数値が出てきたときに戻って来て読みなおすと「なるほど」となるかも.

ふたたび条件付き確率

同時確率を紹介したので, 条件付き確率の定義を話せる. コルモゴロフによる P(B|A) の定義は以下の通り.

\begin{eqnarray} P(B|A) = \frac{P(B,A)}{P(A)} \end{eqnarray}

先ほどの具体例を引っ張り出してくると, 雨の日に事故が発生する条件付き確率P(事故|雨)は

\begin{eqnarray} P(事故|雨) = \frac{P(事故,雨)}{P(雨)} = \frac{\frac{29}{365}}{\frac{100}{365}} = \frac{29}{100} = 0.29 \end{eqnarray}

となる. 分子の同時確率も分母の雨確率も, 数値を入れてみると共通の分母(365)を持つので結局「全雨日数中の事故が起こった日」の割合を見ることになるのがわかると思う.

この数値からどんな意味が読み取れるだろう? 「雨の降っている日に事故の起こる確率」0.29は, 「晴れの日に事故の起こる確率」約0.11*2に比べ2.5倍以上になるので「雨の降っている日は事故が起きやすいので危険ですよ」と言う話を数値で表せたことになる*3.

ここでポイントになるのは, 単純に数値だけを比べると「雨の日は29日事故が起こってるけど, 晴れの日も38日は事故起こってるんだから大したこと無くね?」と勘違いしてしまう可能性があるけれど, 条件付き確率を使えば「雨の日自体が365日中100日しかないんだから, その中の29日は晴れの日とは重みが違うっしょ」ということを数値で語ることができて嬉しい!! というところ.

独立試行と条件付き確率

やや余談.

サイコロを振るとか, コインを投げるとかいった実験は直前に何が出ていようが次の一投には影響せず, 六の目が出る確率は等しく \frac{1}{6}であり, コインが表になる確率は等しく \frac{1}{2}である. こうした前後の試行から切り離されている類の実験を"ベルヌーイ試行"と呼び, それぞれの試行が「独立である」とも言う.

ベン図だと雨ゾーンと事故ゾーンに重なりがないイメージ.

AとBが独立である時, 同時確率は

\begin{eqnarray} P(A,B) = P(A) * P(B) \end{eqnarray}

となる. したがって条件付き確率は

\begin{eqnarray} P(B|A) = \frac{P(B,A)}{P(A)} = P(B) \\ P(A|B) = \frac{P(A,B)}{P(B)} = P(A) \\ \end{eqnarray}

である… 以上.

  • 20150210追記: 独立試行時の同時確率が盛大に間違えてたので修正

ベイズの定理

ようやく本編. とはいえ, ここまでの(1),(2),(3)の知識を使うことでベイズの定理自体はすぐ出てくる.

\begin{eqnarray} P(A|B) = \frac{P(A,B)}{P(B)} \tag{1} \\ P(B|A) = \frac{P(B,A)}{P(A)} \tag{2} \\ P(A,B) = P(B,A) \tag{3} \end{eqnarray}

(3)の条件を当てはめた上で(1)を(2)で割れば \begin{eqnarray} \frac{P(A|B)}{P(B|A)} = \frac{P(A)}{P(B)} \end{eqnarray} となり, これを整理すれば以下の恒等式が導ける.

\begin{eqnarray} P(B|A) = \frac{P(A|B)P(B)}{P(A)} \\ \end{eqnarray}

この関係性が, ベイズが発見しラプラスが広めた「ベイズの定理」である.

ベイズの定理を使ってみる

ベイズの定理を使ってみる. 雨の降る確率がわからない世界線を想定し, その上で, 過去のある日(X年Y月Z日とする)にどのくらいの可能性で雨が降っていたかを見積もりたい.

まず, 何の情報もない状態ではあるが, 雨が降っていた確率を仮に0.1と置く. これはP(雨)であり, ベイズの文脈においては事前確率(prior probability)と呼ばれる.

ここで追加情報が入ってきた. X年Y月Z日の天気は相変わらずわからないが, どうもこの日には事故が発生していたらしい.

事故が起こっている, という前提条件が確定したので, ベイズの定理を使ってP(雨|事故)を求めることが出来る. P(雨|事故)は条件付き確率以外の何者でもないんだけど, ベイズの文脈においては事後確率(posterior probability)とも呼ばれる.

\begin{eqnarray} P(雨|事故)_{事後確率} = \frac{P(事故|雨)P(雨)}{P(事故)} \end{eqnarray}

実際に値を計算してみる. 事故が起こる確率P(事故)0.08と, 雨が降っている時の事故が起こる確率P(事故|雨)0.29は予めわかっているものとする.

\begin{eqnarray} P(雨|事故)_{事後確率} = \frac{0.29 \cdot 0.1}{0.08} \simeq 0.36 \end{eqnarray}

事故が起こったという事実を踏まえ, 雨が降っていた可能性は0.1から0.36へと更新された. 最初に何もわからず0.1と置いたP(雨)よりは, 事故が起こったという事実を踏まえたP(雨|事故)の方が真実に一歩近づいているはず… というのが大枠の使い方*4.

ところで, 上の例で最初に雨が降っていた可能性を0.1と置いたが, 仮に0.2として計算するとP(雨|事故)は0.73となる. このように結果が主観(subjective)によって左右されるところが特徴的で, これが反ベイズ派による批判の的になってきたらしい.

一方で, 「理論的には客観確率が正確ってのはわかるが」「そうは言っても現実の問題をだな」という人は古くからベイズの定理を利用していろいろと成果を上げてきた. そのへんの戦乱(?)の歴史を書いた読み物が 『異端の統計学ベイズ』 で, 面白い本です.

そもそも

上の例イマイチな気がする. 条件付き確率の方と例を揃えようとしたのが悪かったか… より現実的なベイズ用例を探す旅に出ます.

参考(にした)文献

f:id:Hash:20141204010219j:plain

文中にも出たけど, 読み物.

f:id:Hash:20141204010417j:plain

対象はベイズに限らず確率統計全般だけど, 説明がしつこいくらい丁寧で, 手を替え品を替え大量の情報で叩き込んだほうが理解につながる僕のようなタイプにはたいへんありがたい.

余談

今上場してブイブイ言わせている某社がまだ小さかったころ(面接ではないが)ちょっと遊びに行ったら, ホワイトボードにベイズの定理が書いてあり, あれがウチの秘伝公式だよ(笑)とおちょくられた記憶がある.

*1:RubyとRでデータ作成

*2: \begin{eqnarray} P(事故|晴れ) = P(事故|\lnot雨) = \frac{\frac{29}{365}}{\frac{265}{365}} \simeq 0.11 \end{eqnarray}

*3:繰り返しになるが数字は適当. がんばれば 警視庁の事故件数 とか 気象庁の天気履歴 を使って実際のトコロどうなのか調べられそう

*4:だと思っている